Covid-19 様々な実効再生産数とその性質
実効再生産数\(R(t)\)は、一人の感染者が何人に感染させられるかを表す指標である。
時刻\(t\)における新規感染者数を\(I(t)\)とおく。
時刻 \((t-a)\)における一人の新規感染者が、時刻 \(t\)、すなわち、\(a\) 時間後に
新たに一人の感染者を生じる確率を\(g(a)\)とする。この \(a\)は、発症間隔(serial interval)
と呼ばれる。
時刻 \((t-a)\)の新規感染者数は、\(I(t-a) \)だから、時刻 \(t\)における新規感染者の数は、
\(g(a) I(t-a)\) である。この量をすべての \( a>0 \) について加えた(積分)したものが、
一人の感染者が一人の新規感染者を生み出すとした場合の時刻\(t\) における新規感染者数である。
ところが、一人の感染者が一人の新規感染者を生み出すとは、限らないので、この値は、時刻
\(t\)における新規感染者数 \(I(t)\)とは異なる。この値と前者の値の比が実効再生産数 \(R(t)\)
である。すなわち、
\begin{equation}
R(t) = \frac{I(t)}{\int_0^\infty g(a) I(t-a)\, da}
\end{equation}
で与えられる。
実効再生産数についての具体的な計算については、色々な方法が提案されている。そのうちのいくつかを挙げると、
国内の日ごとの新規感染者数と上で述べた4つの実効再生産数を一つのグラフに表す。 新規感染者数については、 厚生労働省のオープンデータを用いる。
実効再生産数についての具体的な計算については、色々な方法が提案されている。そのうちのいくつかを挙げると、
-
Cori et al.の方法
この方法は、上式の\(R(t)\)の右辺の分母に現れる積分を和に置き換えて計算する。 \[ R_C(t) = \frac{I(t)}{\sum_{s=0}^t w_s I(t-s)} \] ただし、\(t\)は、日にちである。 国内におけるオミクロン株の伝染性の確率密度関数については、 国立感染症研究所の推定がある。それによれば、\(g(a)\) は、中央値2.6日のWeibull分布に従う。また、発症間隔の観測データより、 \[ w_0=\frac{1}{30},\ w_1 = \frac{4}{30},\ w_2 = \frac{9}{30},\ w_3 = \frac{8}{30},\ w_4 = \frac{7}{30},\ w_5 =\frac{1}{30} \] である。 -
ロベルト・コッホ研究所 (Robert Koch Institute) の方法
これは、感染間隔の平均日数 \( \tau_g \) (the generation time)におけるウェイトを1、他を0とする。 すなわち、 \[ R(t) = \frac{I(t)}{I(t-\tau_g)} \] オミクロン株の場合は、平均日数を\(\tau_g=2日\)とおくと、 \(\displaystyle R_K(t) = \frac{I(t)}{I(t-2)} \) となる。 -
Bonifazi et al. の方法
上述のコッホ研究所の方法では、新規感染者数に含まれる日ごとのばらつきの影響が大きい場合には、 その影響が実効再生産数にも直接現れるという欠点がある。そこで、Bonifazi等は、新規感染者数についての 7日間の移動平均(moving average)を用いることを提案した。 \begin{eqnarray} R_B(t) & = & \frac{I(t) + I(t-1) + \cdots + I(t-6)}{I(t-2)+I(t-3)+ \cdots + I(t-8)} \\ & = & \frac{\sum_{i=0}^{6}I(t-i)}{\sum_{i=0}^{6}I(t-2-i)} \\ \end{eqnarray} しかし、移動平均で求めるべき値は、中心のデータなので、 \[ I_{MV}(t) = \frac{I(t-3)+\cdots + I(t)+ \cdots + I(t+3)}{7} \] とすべきである。これを用いると、 \[ R_B(t) = \frac{I_{MV}(t-3)}{I_{MV}(t-5)} \] となるので、\(R_C(t)\)や\(R_K(t)\)に比べて3日の遅れが生じる。 -
Nishiura et al.の方法
これは、東洋経済オンラインの 新型コロナウイルス 国内感染の状況で紹介されている方法で、 \[ R_N(t) = \left( \frac{\displaystyle \sum_{i=0}^{\Delta t -1} I(t-i)}{\displaystyle \sum_{i=0}^{\Delta t-1} I(t-\Delta t-i) } \right)^{\frac{\tau_g}{\Delta t}} \] で与えられる。ここに\(\Delta t\) は日にちによる変動を除去するための移動平均の日数で、 7日間の平均移動をとる場合には、\(\Delta t =7\)と置く。さらに、\(\tau_g = 2\)とすると、 上式は、 \[ R_N(t) = \left( \frac{I(t)+I(t-1)+ \cdots +I(t-6)}{I(t-7)+I(t-8)+ \cdots + I(t-13)} \right)^{\frac{2}{7}} \] となる。 ここら辺の解説は、 桂田に詳しい。この方法は、新規感染者数に含まれるノイズに最も影響されにくいという特徴を持っているが、 Cori et al. や Koch研究所の方法に較べて6日の遅れがあるがこの後の解析で分かる。
国内の日ごとの新規感染者数と上で述べた4つの実効再生産数を一つのグラフに表す。 新規感染者数については、 厚生労働省のオープンデータを用いる。
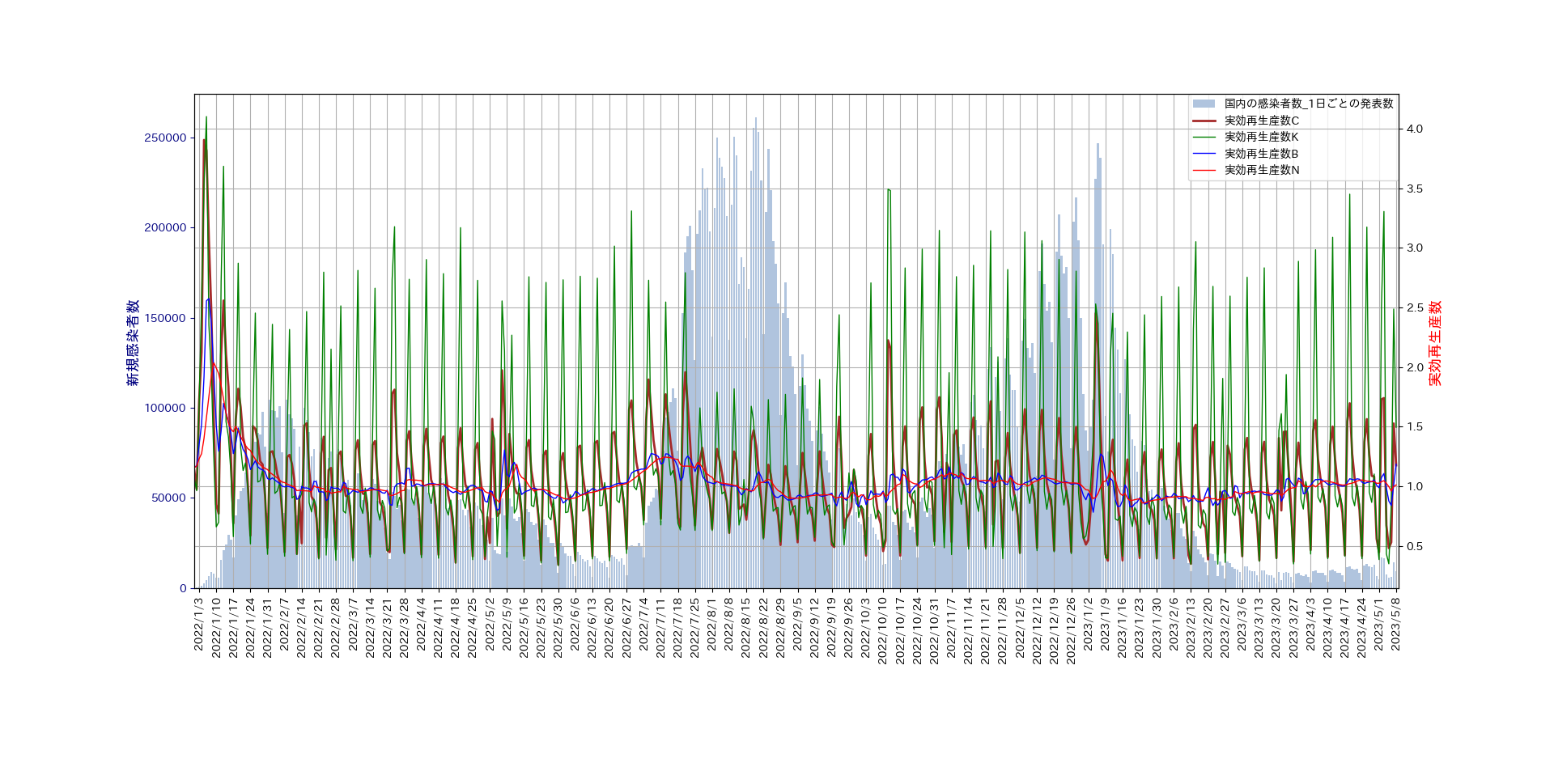
作成したプログラムについては、 ここ をご覧ください。
一見して分かるように、Cori et al.とKoch 研究所の方法では、日ごとの新規感染者に含まれるノイズ
のせいで有効な情報が取り出せない。そこで、新規感染者数についての平滑化を7日間の移動平均を2度行う。
これは中心の重みが最大の3角形となることから、三角移動平均(Triangular Moving Average)と呼ばれる。
こうして得られた新規感染者数を用いて、再び実効再生産数を計算して得られたグラフを以下に示す。
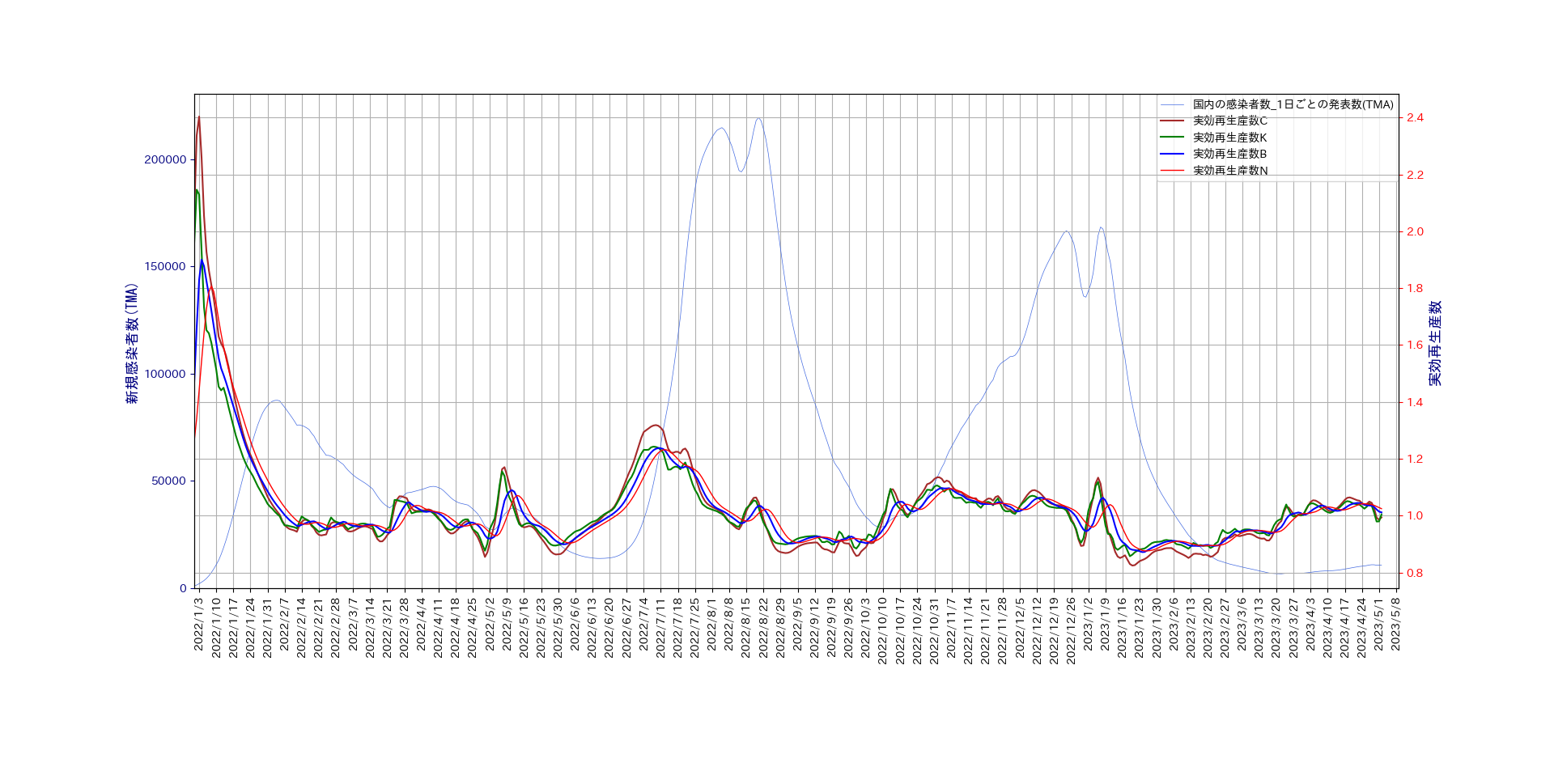
作成したプログラムについては、 ここ をご覧ください。
4つの方法で計算した実効再生産数は、かなり似た振舞いをするようになったが、\(R_B(t)\)と
\(R_N(t)\)は、\(R_C(t)\)と\(R_K(t)\)に較べて時間に遅れががあるように思われる。そこで、
\(R_B(t)\)を左に1日、\(R_N(t)\)を左に6日ずらしてグラフを描き直す。
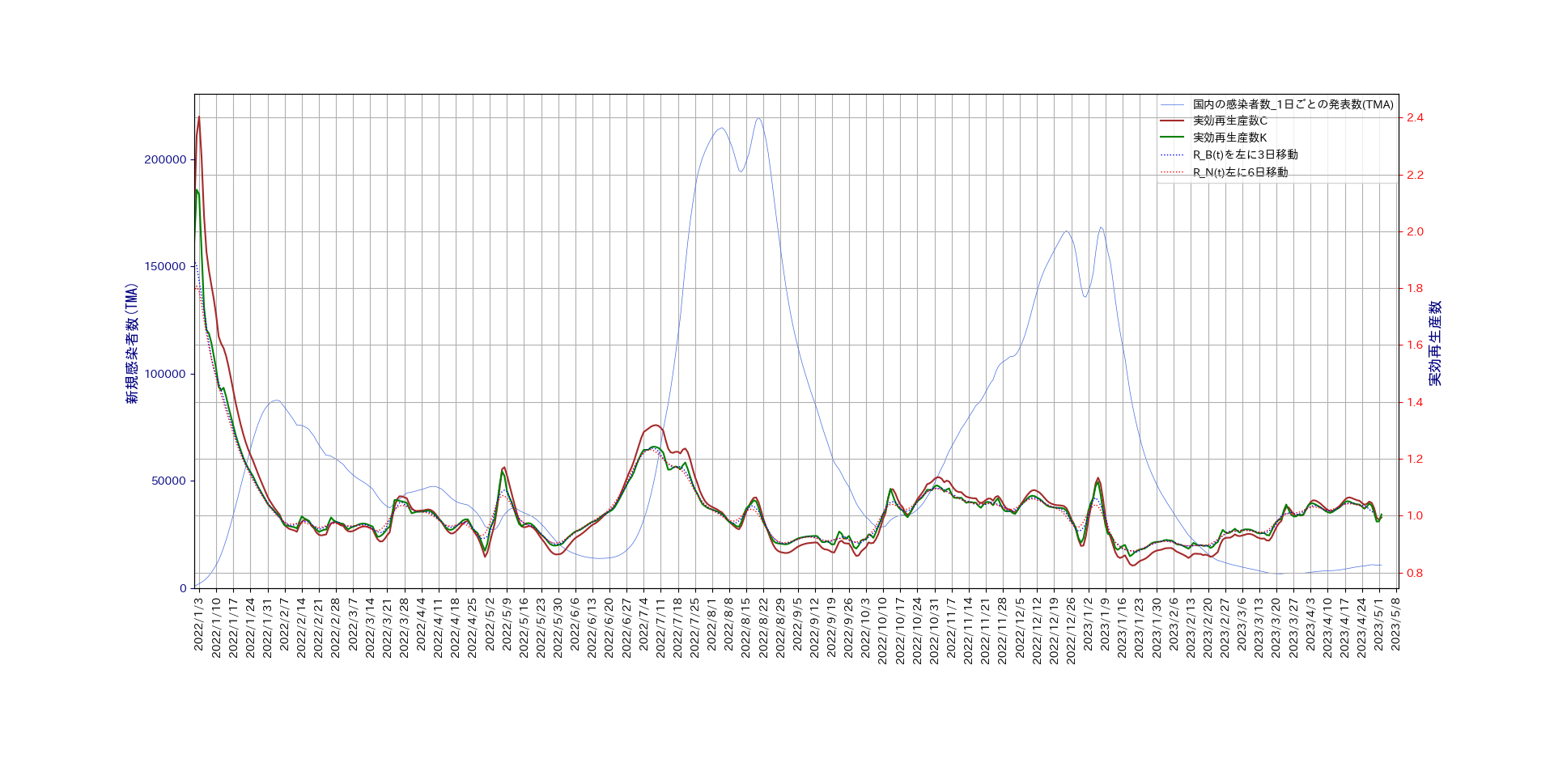
作成したプログラムについては、 ここ をご覧ください。
今度は、4つの方法の計算での山と谷の時間が一致していることが分かる。これらの結果を用いて、
\[
\frac{d I(t)}{dt} = \gamma \left(R(t) -1 \right) I(t)
\]
が成り立つかを調べる。そのためには、時間 \(t\) を離散化
\( (t= 0, \ 1, \ 2 \cdots,\ i, \ \cdots) \)
し、\(\Delta t =1 \) とおいて、等式
\[
I(i+1) - I(i) = \gamma \left( R(i+1) -1 \right) I(i)
\]
が成り立つかを調べる。ただし、\(R_B(i)\) と \(R_N(i)\) については、時間の遅れを考慮して、
それぞれ、\(R_B(i+4)\)、\(R_N(i+7)\)とする。以下に\( \gamma = 1/3\) の結果を示す。
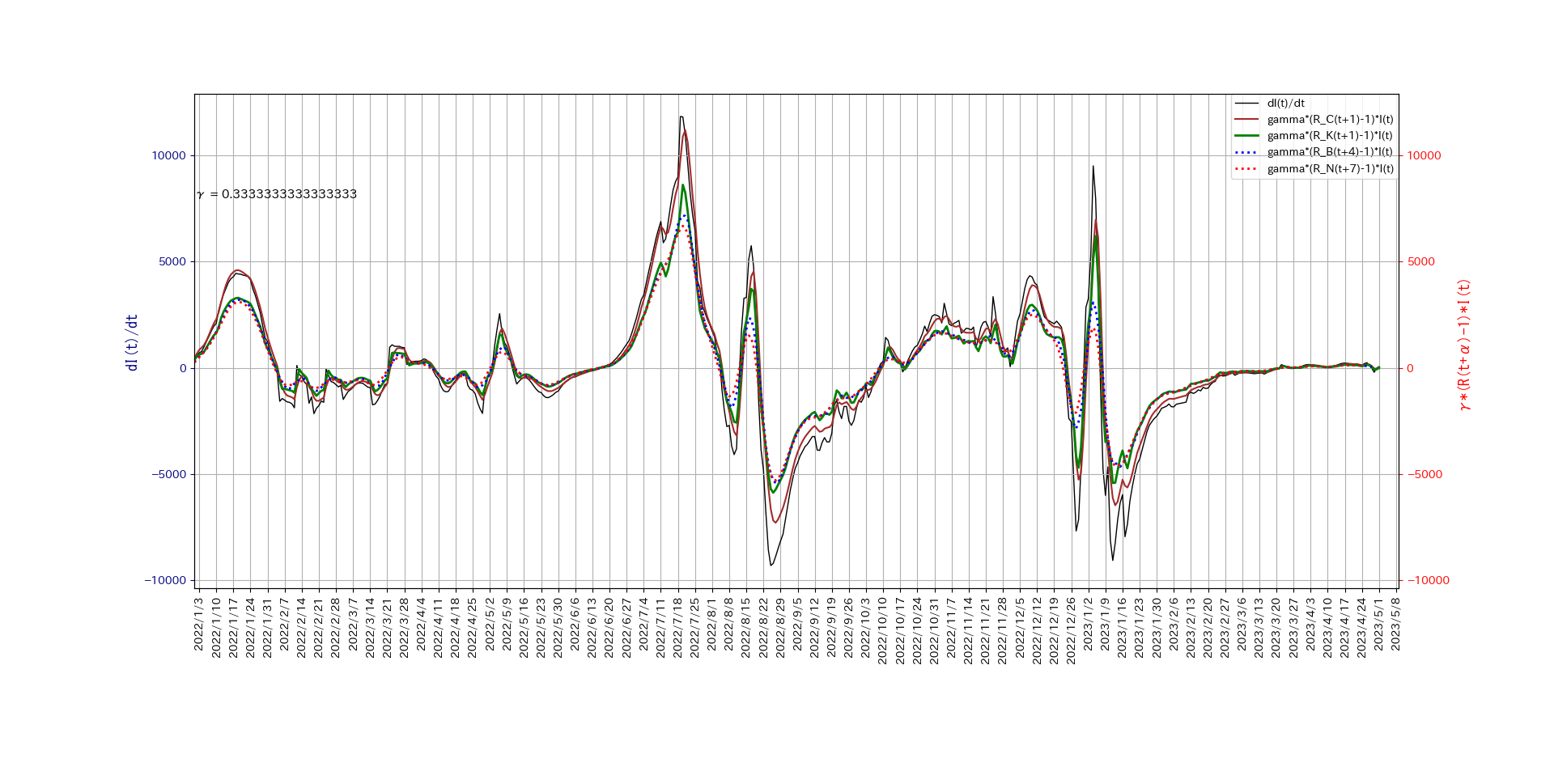
4つの方法は、いずれも関係式
\(\displaystyle
\frac{d I(t)}{dt} = \gamma \left(R(t) -1 \right) I(t)
\)
を概ね満たすことが分かる。特に、Cori et al.の方法が、手間がかかる分だけ
優れているように思われる。この方法が、標準として
用いられる所以である。
【付記】(2023/1/26)
Nishiura等の公式、 \[ R_N(t) = \left( \frac{\displaystyle \sum_{i=0}^{\Delta t -1} I(t-i)}{\displaystyle \sum_{i=0}^{\Delta t-1} I(t-\Delta t-i) } \right)^{\frac{\tau_g}{\Delta t}} \] は、 \begin{equation} R_N\left( t-\Delta t + \frac{\tau_g+1}{2} \right) = \left( \frac{\displaystyle \sum_{i=0}^{\Delta t -1} I(t-i)}{\displaystyle \sum_{i=0}^{\Delta t-1} I(t-\Delta t-i) } \right)^{\frac{\tau_g}{\Delta t}} \label{eq:R_Nnew} \end{equation} と修正されるべきである。
ここで、オミクロン株の場合に合わせて、 \(\tau_g = 2, \ \Delta t = 7\)とすると、 \[ R_N(t-5.5) = \left( \frac{I(t) + I(t-1) + \cdots + I(t-6)}{I(t-7) + I(t-8) + \cdots + I(t-13)} \right)^{2/7} \] を得る。
導出方法については、 再生方程式と実効再生産数 を参照のこと。
【付記】(2023/1/26)
Nishiura等の公式、 \[ R_N(t) = \left( \frac{\displaystyle \sum_{i=0}^{\Delta t -1} I(t-i)}{\displaystyle \sum_{i=0}^{\Delta t-1} I(t-\Delta t-i) } \right)^{\frac{\tau_g}{\Delta t}} \] は、 \begin{equation} R_N\left( t-\Delta t + \frac{\tau_g+1}{2} \right) = \left( \frac{\displaystyle \sum_{i=0}^{\Delta t -1} I(t-i)}{\displaystyle \sum_{i=0}^{\Delta t-1} I(t-\Delta t-i) } \right)^{\frac{\tau_g}{\Delta t}} \label{eq:R_Nnew} \end{equation} と修正されるべきである。
ここで、オミクロン株の場合に合わせて、 \(\tau_g = 2, \ \Delta t = 7\)とすると、 \[ R_N(t-5.5) = \left( \frac{I(t) + I(t-1) + \cdots + I(t-6)}{I(t-7) + I(t-8) + \cdots + I(t-13)} \right)^{2/7} \] を得る。
導出方法については、 再生方程式と実効再生産数 を参照のこと。