注： 2022年9月26日より、厚生労働省は新型コロナ感染者の全数把握の簡略化を開始しました。 それに伴い、NHKでは9月28日以降については「データのダウンロード」を停止しました。そこで、以下では NHKから提供のあった9月27日までのデータ解析の結果を掲載します。
　ついでに、数値などのタイプミスの修正も行いました。

　2022年7月よりcovid-19の第7波が始まりました。2022年1月に始まった第6波以降の１日ごとの感染者 の推移と共に実効再生産数をグラフで表すと以下のようになります。 今までと同様に、１日ごとの規感染者数については、NHKの NHK特設サイト 新型コロナウイルス から、データをダウンロードして使用します。
　実効再生産数については、東洋経済onlineの 新型コロナウイルス 国内感染の状況 から、日別全国の実効再生産数(effective_reproduction_number.csv)をダウンロードします。 ダウンロードしたデータはメモ帳で開いてエンコードをANSIにして保存し直します。
　2022年1月に始まった第6波以降の１日ごとの感染者数 の推移と共に実効再生産数をグラフで表すと以下のようになります。

　最近では、covid-19における感染の広がりの解析を数理モデルを用いて行おうとする 機運は薄れつつあります。理由は色々あるでしょうが、一つには、代表的なSIRモデルは、確定的 であることが挙げられます。すなわち、全てのふるまいは初期値を与えることによって、全てが 決まってしまいます。我々は、感染が広がると、マスクをしたり、人混みの中に出かけないとか、 ワクチン接種を受けるとか、何らかの防衛策を講じます。こうして実効再生産数を制御することが できます。それを考慮するためには、実効再生産数を外部パラメータとして導入する必要があります。
　ここでは、第6波から第7波において、表題の関係が成り立っているかを調べます。
　上の図では、曜日による変動など、細かな変動のために全体の傾向がつかみにくくなっています。 そこで、日ごとの感染者数については、7日間の移動平均を2回行うことにします。これは、加重移動平均 (三角移動平均 Triangular Moving Average (TMA))に相当します。また、対応する実効再生産数の 細かな変動も、7日間移動平均を取ることにより、平滑化することにします。すなわち、我々が解析 するモデルは、次の図で与えられます。

　新規感染者数についてはNHKのデータを、実効再生産数については東洋経済オンラインのデータを用いて、 \(I(t)\)と\(R(t)\)の関係、 \[ \frac{d I(t)}{dt} = \gamma \left(R(t) -1 \right) I(t) \] が成り立つかを調べます。 ただし、\(I(t)\)は、感染者数ではなく、新規感染者数とします。 データは日ごとに与えられているので、実際には、上式で \(dt = 1日 \) と取って差分で扱います。すなわち、\(i\)日目のデータについて、 \[ I(i+1) - I(i) = \gamma \left(R(i) -1 \right) I(i) \] が成り立つかを調べます。ここで、\(\gamma = 1/4\) とした場合の結果は、以下の通りです。 この図からは、第6波の最初の大きな山は、大体合っているいるが、それ以降は、全く合っていないのが 分かります。特に、\(R(i) -1 = 0 \)となる\(i\)の値が\(I(i+1) - I(i)\)となる\(i\)の値よりも 7日程度後ろにずれていいるのが、分かります。

　そこで、\(R(i)\) を \(R(i+7)\) で置き換えた式、 \[ I(i+1) - I(i) = \gamma \left(R(i+7) -1 \right) I(i) \] が成り立つかを調べてみました。全体のスケールを合わせるために、今度は\(\gamma = 1/2\)としました。 結果は、以下の通りで、第6波の最初を除いて、良く合っているのが分かります。

【注】上記結果を得るためには、covid19_main1.py，covid19_main2.py，covid19_main3.py のプログラムを順次実行する必要があります。

　ついでに、第1波から第5波についても同様の解析を行いました。 新規感染者数については7日間移動平均を2回行い、実効再生産数については、 7日間移動平均1回行うことにより平滑化することにします。次の図は、そのようにして得られたものです。

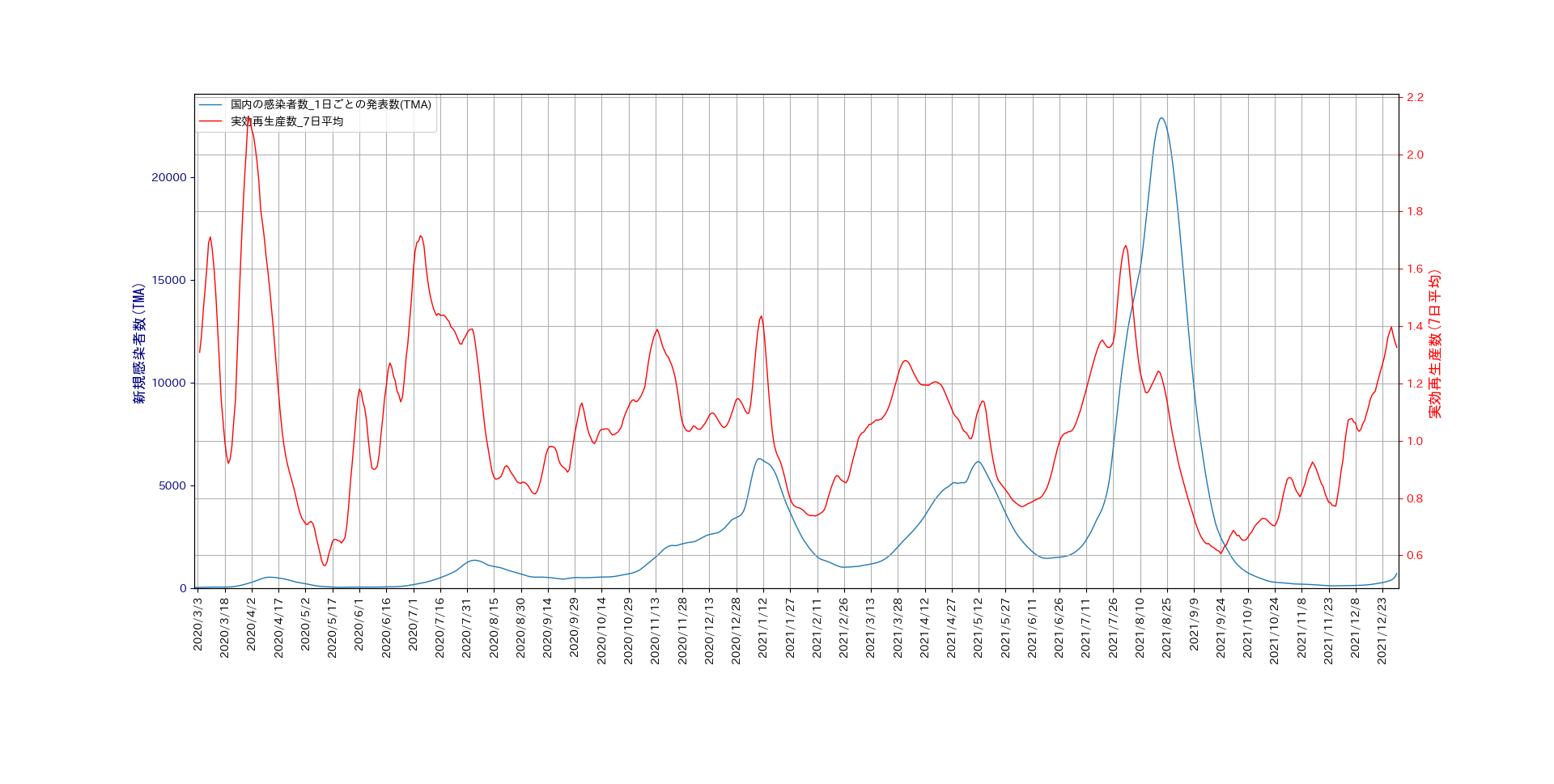
　得られたデータについて、 \[ I(i+1) - I(i) と \gamma \left(R(i+7) -1 \right) I(i) \] をプロットして比較してみます。ただし、今度は\(\gamma = 1/5 \)としました。

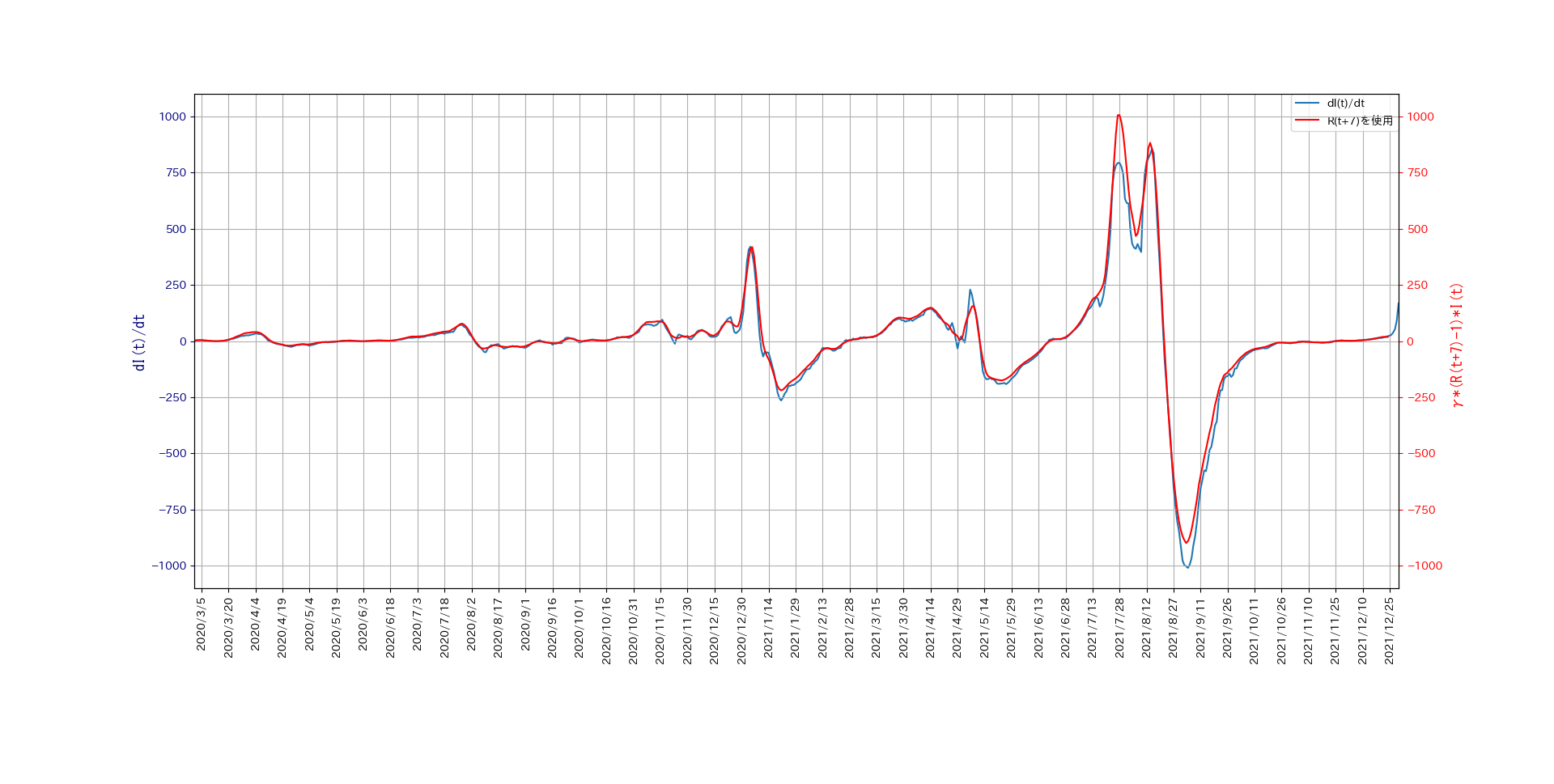
　以上の結果から、以下のことが分かります。
時間\(t\)を日にちとすると、関係式 \[ I(t+1) - I(t) = \gamma \left(R(t+7) -1 \right) I(t) \] が成り立つ。ただし、第1波から第5波までは\(\gamma = 1/5 \)と、第6波以降は \(\gamma = 1/2\)とする。ここで、\(\gamma\) の値の違いは、変異株の性質によるものと 思われる。
　上式は、SIRモデルを一般化したものである。なぜ、この式が成り立つか、 特に、なぜ\(R(t+7)\)かは、もう少し、考えてみる必要がありそうです。

　その後、様々な実効再生産数について調べた結果、西浦等の方法による東洋経済オンラインデータには、 スタンダードであるCori等の結果と比べて6日の遅れがあることが分かりました。Cori等の方法による実効再生産数を用いると、 \[ I(i+1) - I(i) = \gamma \left(R(i+1) -1 \right) I(i) \] すなわち、 \[ \frac{d I(t)}{dt} = \gamma \left(R(t) -1 \right) I(t) \] が成り立つことが分かりました。

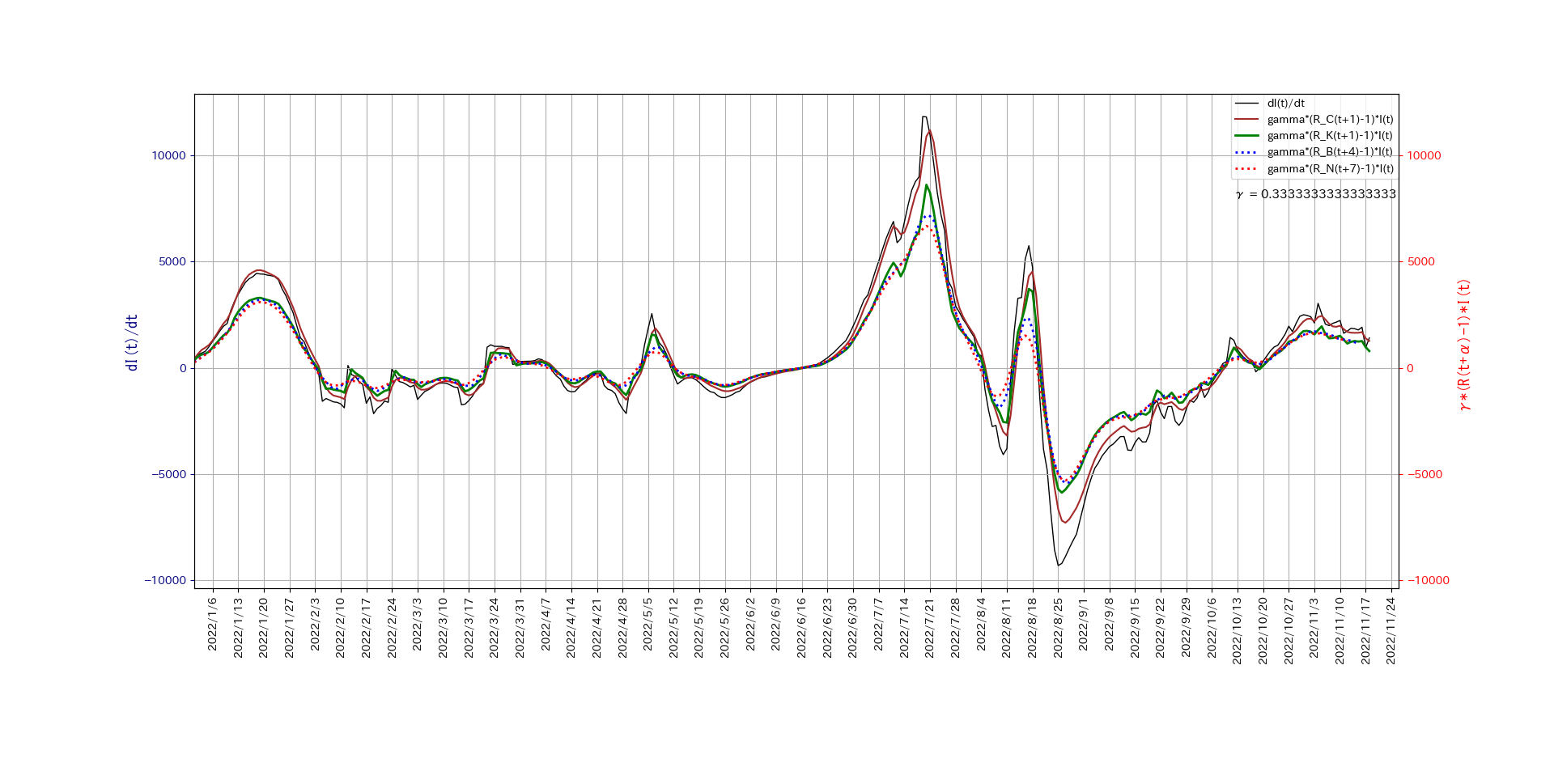
　詳しくは、 Covid-19 様々な実効再生産数とその性質 をご覧ください。